Quelques exemples d'utilisation
| Mon poids – ma masse ? 2 masses m1 et m2 dans l'espace, dont leur centre de gravité est distant de ΔL, s'attirent réciproquement avec une force de gravitation F, dont la valeur absolue |F| vaut : |F|=G.m1.m2/ (ΔL)2 Cas particulier d'une personne de masse m, et de la terre de masse Mt. Mt et m sont donc à une distance égale au rayon terrestre Rt. |F|=G.m1.m2/ (ΔL)2 = G.m.Mt/(Rt)2= m.G.Mt/(Rt)2 Avec m1, masse de la personne = m , m2=Mt, et ΔL=Rt G est le coefficient d'attraction universel, qui vaut 6,67 10-11 m3/kg.s2 Mt vaut 5,972.10+24 kg, Rt vaut 6371 km, soit 6,371 10+6 m Dans ce cas, |F| s'appelle le poids P Calculons G.Mt/(Rt)2 qui est une valeur presque constante à la surface de la terre, et nommons g cette valeur. Il s'agit ici de l'accélération de la pesanteur terrestre. L'unité de g sera donc en (m3/kg.s2).kg/m2, c'est à dire en m/s2. Il s'agit bien d'une accélération. g= G.Mt/(Rt)2 = 6,67 10-11 . 5,972.10+24 / (6,371 10+6)2 = 6,67.5,972/(6,371)2 . 10+7 = 9,81 finalement g = 9,81 m/s2. On arrondit souvent à 10 cette valeur. Et la force devient P=m.g Une personne de masse 80 kg a un poids à la surface de la terre d'environ 800 N (785 Newton exactement). Nos balances sont graduées approximativement en 1/10ème de Newton, improprement nommés kg. A la surface de la lune, l'accélération est de 1,622 m/s2. La pesanteur lunaire est donc 9,81/1,62 = 6 fois moins élevée qu'à la surface de la terre. Le poids de la même personne serait de P=80.1,622 = 130 N. La force exercée sur le plateau de la même balance est donc 785/130 = 6 fois moins élevé. L'indication de la balance serait donc de 130/10 = 13 kg, manière de dire que la personne pèserait 6 fois moins sur la lune que sur la terre... ...tout en gardant la même masse de 80 kg ! |
| Dans l'espace : vitesse de libération ? Si je jette une pomme en l'air, elle retombe devant moi. Mais si je la jette devant moi avec suffisamment de force (en supposant les forces de frottement dans l'air négligeables), elle peut atteindre une telle vitesse qu'elle fait le tour de planète avant de revenir sur moi de l'autre côté ! Si je la jette encore plus fort, elle pourrait même se libérer complètement de la force d’attraction gravitationnelle de la terre ! Bien sûr, pour une pomme, à cause de sa faible densité, c'est difficile à imaginer... mais pour une fusée, c'est possible. A partir de quelle vitesse une fusée de masse m peut-elle s'échapper de l'attraction terrestre ? Son énergie potentielle à la surface de la terre est Ep= m.g.Rt = m. G.Mt/(Rt)2 . (Rt), soit Ep= m. G.Mt/Rt. Son énergie cinétique est Ec = ½ m . v2 Au moment de la libération, la vitesse v atteinte est telle que l'énergie cinétique équilibre l'énergie potentielle, et Ep=Ec. On a alors : Ep= m. G.Mt/Rt = ½ m . v2 = Ec Donc en simplifiant par m : G.Mt/Rt = v2/2, et donc v2 = 2.G.Mt/Rt v2= 6,67 10-11 . 5,972.10+24 / (6,371 10+6) = 1,25 10+8, donc v=√(v2)= √1,25 . 10+4 = 1,11 10+4 m/s, soit environ 11,1 km/s, soit environ 40 000 km/h. Ainsi, nos fusées doivent atteindre cette vitesse quand elle veulent rejoindre notre satellite, la lune !  Pour atteindre de telles vitesses, 3 étages n'étaient pas de trop pour la fusée Saturne V – APOLLO. Le premier étage avait une poussée équivalente à 4 réacteurs de Concorde et envoyait la fusée à 60km d'altitude en 150 secondes, à la vitesse de 9600 km/h. Le deuxième étage prenait le relais, et 450 secondes plus tard, à 173 km d’altitude, la vitesse atteignait les 27800 km/h. Restait le 3ème étage, pour atteindre la limite fatidique... ....tout en gardant suffisamment de carburant pour la mise en orbite lunaire et le voyage retour. Des calculs analogues de vitesse de libération donneraient une vitesse de 2,4 km/s (8600 km/h) pour s'échapper de l'orbite de la lune, de 42,1 km/s pour s'échapper du système solaire depuis la terre et de 617 km/s si la fusée s'échappait directement du système solaire depuis... le soleil. |
| L'astronautique et l'énergie Les cinq moteurs F-1 utilisés sur Saturn V, mis au point par les équipes de Werner Von Braun, brulaient de l'oxygène liquide (LOX) et du kérosène (RP-1) Caractéristiques du moteur F-1 : un poid d'un peut plus de 8 tonnes. Une consommation de presque 3 tonnes de de kérosène et d'oxygène liquide par seconde, et cela pendant une durée de 165 secondes. Le résultat : une poussée de 6700 kN (680 tonnes) Une puissance de 24 GW, soit 32 millions de chevaux-vapeur !
 Ce même mélange était utilisé pour la fusée Soyouz. Ici le lancement de la mission TMA-18 le 02/04/2010. Propulseur d'appoint : 1000 kN de poussée, durant 120 s ( Impulsion spécifique Is = 310 s) 1er étage : 1000 kN de poussée, durant 300 s ( Impulsion spécifique Is = 310 s) 2ème étage : 300 kN de poussée, durant 300 s ( Impulsion spécifique Is = 360 s) L'impulsion spécifique indique la durée pendant laquelle un kilogramme de propergol (notre mélange kérosène + oxygène liquide) produit une poussée permettant de déplacer une masse d'un kilogramme (soit une force d'environ 9,81 N) dans le champ gravitationnel terrestre : Is= F/q.g avec F la poussée (en N), q le débit massique d'éjection des gaz (en kg/s) et g l'accélération de la pesanteur (en m/s² ou N/kg). On peut déduire de ce qui précède le débit massique d'éjection des gaz En prenant Is=375 s pour le RP-1, la plus grande valeur pour un réacteur kérosène + oxygène liquide, on a Is= F/q.g, donc q= F/Is.g = 6700 000 / 375.10 = 1786 kg/s Inversement, en prenant q=3000 kg/s pour le RP-1, on peut en déduire l'impulsion spécifique Is= F/q.g = 6700 000 / 3000.10 = 223 s Cet exemple montre l'intérêt de croiser les données de la littérature. En effet, celle-ci ne donne pas toujours des données absolument exacte, car les phénomènes réels sont plus complexe que les équations simplifiées au premier ordre des modèles. * * * Application numérique Pour un moteur F-1 : P=W/ Δt, soit : 24 000 000 000 = W / 150 W = 3600 000 000 000 Joules = 3600 GJ, soit 1 000 000 kWh = 1000 MWh = 1 GWh
Partons de la poussée au décollage qui nous est donnée. Cette poussée est engendrées par 5 moteurs F-1. 3500 tonnes de poussée au décollage, avec une masse au décollage de 3000 tonnes F fusée = 3 500 000 . 9.81 = 34 MN ou encore F fusée = 6700 kN . 5 = 34 MN environ Jusqu'à quelle distance peut théoriquement aller ce 1er étage ? En supposant la poussée constante (ce qui est une approximation du premier ordre), W=F. ΔL 3600. 10+9 . 5 = 34 10+6 . ΔL ou encore 3600 000 000 000 Joules x 5 = 34 000 000 . ΔL ΔL = 530 000 m =530 km En fait, la poussée va diminuer au fur et à mesure, et la distance sera moindre.
Déterminons l'accélération au décolage. F=m.a, avec une masse au décollage de 3000 tonnes 6 700 000 x 5 = 3 000 000 . a a =11,16 m/s2 env. soit 1,13 g. C'est effectivement un valeur voisine de l'accélération au décolage.  Et a quel moment la fusée atteindra t'elle l'altitude de séparation du 1er étage ? La solution est donnée par l'équation L=V.T = ½ a. t2 Donc, en supposant l'acceleration constante (ce qui est inexact mais donne l'ordre de grandeur), après une durée permettant de parcourir une distance comprise entre 113 km (la distance réelle) et 530 km (la distance maximum théorique) 113 000 = 11,2/2. t2 ... donne t = 142 s 530 000 = 11,2/2. t2 donne ... t = 307 s Le moment réel est connu : 165 s L'intérêt de cet exemple est de montrer qu'avec des "calcul de coin de table", sans connaitre les équations exactes qui tiennent compte de nombreux facteurs (variation des frottements avec l'altitude, diminution progressive de la masse, épuisement du carburant...) on arrive a des résultats du bon ordre de grandeur. sources indicatives : http://fr.wikipedia.org/wiki/Saturn_V http://wechoosethemoon.org http://www.youtube.com/watch?v=IkS4Dfi2m10 |
| L'énergie d'une balle de fusil Prenons une carabine (typiquement le FRF1 de l'armée française) dont le canon fait 60 cm de long, et qui tire des projectiles de 9 grammes (typiquement 7,62 Otan). La vitesse atteinte à la sortie du canon est de 780 m/s.  L'énergie cinétique de la balle est Ec=1/2. m. v2 = ½ . 0,009. 780.780 = 2738 Joules. La balle en sortie de canon de longueur ΔL = 0,6 m, a effectuée un travail de W=F. ΔL équivalent à cette énergie cinétique. W=2738 Joules, soit 2738/3600 = 0,76 Wh La force F exercée sur le projectile (sa poussée) est donc: F= W/ ΔL de F = 2738/0,6 = 4563 Newton (soit environ 465 kg de poussée) L'accélération a du projectile est donnée par l'équation F=m.a On a donc a= F/m = 4563/0,009 = 507000 m/s2 environ, soit environ 52 000 g ! L'équation du mouvement donne L = 1/2. a . t2 La balle sort du canon au bout du temps t = √ (2.L/a) = √ (2.0,6/507000) = 0,0015 s, soit un peut plus de 1 millième de secondes. Compte tenu de la vitesse de sortie du canon qui est de 600 m/s, on a bien une accélération de a= ΔV/ Δt = (780-0)/(0,0015-0)=507000 m/s2  La loi de conservation de la quantité de mouvement nous permet de calculer la vitesse de recul du fusil dont on va supposer qu'il a une masse de 5,125 kg. m projectile . v projectile = m fusil . v fusil, soit : 0,009 . 780 = 5,125 . v fusil la vitesse de recul du fusil est donc égale à 0,009.780/5,125 = 1,37 m/s, soit 4,9 km/h |
| Tir à l'arc et énergie Prenons l'arc longbow que les archets gallois et anglais utilisèrent à la bataille d'Azincourt en 1415. Sa puissance est de 530 à 580 Newton (entre 50 et 60 kg force, soit 120 à 130 livres), alors que les arcs modernes ont une puissance maximale moitié moindre (entre 25 livres pour une faible puissance à 50 livres pour une bonne puissance).  La masse de l'arc est d'environ 600g (compter un kilo de plus pour un arc moderne). Son allonge est de 70 cm (distance entre corde tendue et corde au repos au point d'accroche de la flèche). La masse de la flèche est de 70 g (alors que les flèches modernes font plutôt autour de 20 g). La vitesse de la flèche en sortie d'arc est de 55 m/s (200 km/h) On supposera que la vitesse moyenne de la flèche durant le parcours qui va de sa phase d'immobilité à la vitesse atteinte lorsqu'elle quitte l'arc est de la moitié de sa vitesse de sortie, soit <v> = 55/2 = 27,5 m/s (en effet, la tension de la corde part d'un maximum pour atteindre son minimum au départ de la flèche). L'énergie cinétique de la flèche est Ec=1/2. m. v2 = ½ . 0,07. 55.55 = 106 Joules. La flèche en sortie d'arc d'allonge ΔL = 0,7 m, a effectué un travail de W=F. ΔL équivalent à cette énergie cinétique. W=106 Joules, soit 106/3600 = 0,029 Wh La force F exercée sur le projectile (sa poussée) est donc F= W/ ΔL de F = 106/0,7 = 151 Newton (soit environ 15 kg de poussée) et sa quantité de mouvement p=m.v = 0,07.55=3,9 kg.m/s L'accélération a du projectile est donnée par l'équation F=m.a On a donc a= F/m = 151/0,07 = 2150 m/s2 environ, soit environ 220 g ! L'équation du mouvement donne L = 1/2. a . t2 La flèche sort de l'arc au bout du temps t = √ (2.L/a) = √ (2.0,7/2150) = 0,0255 s, soit un peut plus de 2 centièmes de secondes. On a aussi L = v.t, avec v= vitesse moyenne = 27,5 m/s, soit t=L/v=0,7/27,5 = 0,0255 s. Compte tenu de la vitesse de sortie d'arc qui est de 55 m/s, on a bien une accélération de a= ΔV/ Δt = (55-0)/(0,0255-0)=2155 m/s2 La loi de conservation de la quantité de mouvement nous permet de calculer la vitesse de recul de l'arc dont on va supposer qu'il a une masse de 0,6 kg. m projectile . v projectile = m arc . v arc, soit : 0,07 . 55 = 0,6 . v arc La vitesse de recul de l'arc de 600 g est donc égale à 0,07.55/0,6 = 6,4 m/s, soit 23 km/h La vitesse de recul d'un homme de 70 kg serait quant à elle de : 0,6.6,4/70 = 0,055 m/s, soit 0,2 km/h La puissance développée par l'arc pendant le tir est P=W/ Δt = 106 Joules/0,0255 s = 4150 watts. Un homme à la force des bras peut déployer au maximum dans sa journée jusqu'à 0,05 kWh, soit 50 Wh (le 1/10ème de ce qu'il peut déployer avec ses jambes). Un combattant tirait environ 16 minutes à une cadence de 10 flèches par minute (600/h), et dépensait donc une énergie de 106 Joules. 10.16 = 16960 Joules = 4,7 Wh durant 16 min, soit un dixième de sa dépense énergétique musculaire de sa journée en l'espace de 16 minutes. Il développait pour cela avec la force de ses bras une puissance de P=16960/(16*60) = 18 watts. (avec ses jambes 10 fois plus puissantes que ses bras, un cycliste peut aller jusqu'à quelques centaines de Watt) Un tireur contemporain, qui tirerait à l’entraînement 100 flèches en 1 heure dépenserait en une heure une énergie de 106 Joules x 100 = 0,029 W.h x 100 = 2,9 Wh. Un tel exercice durant 8 heures lui coûterait environ 23 Wh, ce qui est considérable... même si cela ne représente environ que 200 fois moins que l'énergie que peut fournir un seul litre de pétrole (environ 10 000 Wh x rendement mécanique minima de 50% = 5000 Wh) . |
| de l'arc au fusil... une question d'énergie et de poudre noire... la poudre a canon a rendu possible : la multiplication par plus de 26 de l'énergie du projectile : de 0.029 Wh à 0.76 Wh la multiplication par plus de 14 de la vitesse du projectile : de 55 m/s à 780 m/s Tout cela grace à la chimie : La poudre noire est un mélange de 75% de salpêtre (nitrate de potassium KNO3), de 10% de soufre et de 15% de charbon de bois. Cette poudre est un mélange de deux éléments très combustibles (le soufre et le charbon), avec un corps très oxydant : le salpêtre. * * * Le Salpêtre se forme sur les vieux murs humides, surtout quand l'eau, qui remonte par capillarité le long des murs, est riche en nitrate. Le salpêtre est l'un des résidus du développement de bactéries qui se nourrissent de l'ammoniaque provenant de l'eau du sol et du carbonate de potassium contenu dans les murs. - Le Soufre se trouve natif dans la nature, dans des gisements d'où il peut être extrait. - Le charbon provient du bois d'arbres (peuplier, tilleul). A une température de 300-350 °C, on obtient du charbon. * * * Un kilogramme de poudre libère environ 350 litres de produits gazeux. La réaction est très exothermique, et la température de l'explosion atteint 2 400 °C. 2 KNO3 + S + 3 C → K2S + N2 + 3 CO2 ΔrH°(923K)=−653,7kJ/mol KNO3 : 101 g/mole, S : 32 g/mole , C : 12g/mole Dans les proportions stoechiométriques : 2 KNO3 : 202/270=75% ; S : 32/270=12% , 3 C: 36/270=13% 1 mole de poudre fait donc : 2.101+1.32+3.12=270 g Une mole de poudre produit donc : 1 mole d'azote, soit 28 g à 1.185 kg/m3, soit 23.6 litres + 3 mole de CO2, soit 44 . 3= 132 g à 1.87 kg/m3, soit 70.5 litres ... soit en tout 94,1 litres Donc 1 kg de poudre produit 94,1.1000/270= 350 litres de gaz. C'est cette expansion exothermique qui va propoulser la balle dans le canon.... |
| Chimie, radioactivité, fission, fusion nucléaire ... et énergies H est l'atome d'Hydrogène. Son noyau est composé d'un unique proton (de charge +1), et un électron tourne autour de ce noyau (de charge -1). Il y a toujours autant de protons que d'électrons dans un atome. C est l'atome de Carbone. Son noyau est composé de 6 protons et de plusieurs neutrons (de 5 à 8), et de 6 électrons qui tournent autour du noyau. Le noyau a donc : ou 6 protons + 5 neutrons = 11 nucléons. C'est le Carbone 11, qui est instable (radioactif, traces) ou 6 protons + 6 neutrons = 12 nucléons. C'est le Carbone 12, qui est majoritaire (99% dans la nature) ou 6 protons + 7 neutrons = 13 nucléons. C'est le Carbone 13, qui est stable (1% dans la nature) ou 6 protons + 8 neutrons = 14 nucléons. C'est le Carbone 14, qui est instable (radioactif, traces) Le Carbone 12 est par exemple noté 12C, et le carbone 14 est noté 14C.  Quand un atome est instable, on dit qu'il est radioactif, et il se décompose en éléments stables au cours du temps, selon un rythme qui dépend de sa période, c'est à dire de sa demi-vie. Par exemple, le Carbone 14 à une demi-vie de 5730 ans, ce qui signifie que au bout de cette durée, la moitié des atomes de carbone 14 présents dans l'échantillon étudié se seront décomposés (on dit désintégrés) en autre chose (en azote 14 pour le cas du carbone 14, en Bore 11 pour le carbone 11) : 14C → 14N + -1e : émission d'un électron  Sachant que le 14C se forme aussi de manière naturelle... à partir de 14N !  11C → 11B + +1e : émission d'un positon, sachant que -1e + +1e → γ (rayon gamma = photon de haute énergie) l'antimatière (le positon) ne reste en effet pas longtemps dans la nature... elle s'associe rapidement avec la matière (ici l'électron) ... et donne de l'énergie Le Carbone a 6 électrons, dont 2 proches du centre de l'atome, et 4 sur la périphérie par l'intermédiaire duquel l'atome va pouvoir se lier à d'autres atomes. On dit que le carbone est tétravalent (de valence 4) Les 2 électron du centre... restent au centre au sein d'une zone appelée orbitale intérieure (orbitale 1s), qui est plus stable (faible énergie) ... et les 4 de la périphéries se balladent au sein de zone spatiales imaginaires (qui reflètent un nuage de probabilité de présence autour du noyau), dans des "orbitales extérieures" en forme de sphère (2s) ou de sablier 2p), attendant de se lier à un autre atome
Une liaison chimique est la mise en commun d'électron, l'un provenant d'un atome, et l'autre d'un autre, ou les 2 électron provenant d'un seul atome qui les dédie à la relation Par exemple, chacun des électrons libres de l'atome de Carbone excité se lie à l'électron de l'atome d'hydrogène... ... pour donner la molécule de méthane : CH4  Les molécules : Ce sont des associations d'atomes, comme on le ferait avec des LEGO. Certains atomes ont 1 seul point d'accrochage (une patte, ou encore une valence de 1), d'autres en ont 2, d'autres 3, d'autres 4, etc... Par exemple, l'Hydrogène H en a 1. L’ Oxygène O en a 2 le plus souvent, l' Azote N en à 3, le Carbone en a 4. * * * Exemples : CO2 est le gaz carbonique, encore appelé dioxyde de carbone. CO2 : O=C=O : les atome sont sur une droite. Les pattes des Oxygènes sont reliés aux pattes du carbone. CH4 est le Méthane, c'est le gaz de ville. H | CH4 : H-C-H | H Les H sont les sommets d'une pyramide dont le C est le centre.  H2O est l'eau. H2O : H-O-H :les H sont 2 sommets d'une pyramide dont le O est le centre NH3 est l’ammoniac. N2 est l'azote : N≡N . chacun des atomes est relié à l'autre par ses 3 pattes. NH3 : les H sont 3 sommets d'une pyramide dont le N est le centre. * * * Des réactions chimiques sont possibles, comme par exemple : La combustion du méthane dans l'oxygène, qui donne du CO2, de l'eau... et de l'énergie ! À 1 bar et 25°C : CH4 + 2 O2 → CO2 + 2 H2O + 803 kJ/mole (891 kJ/mole si l'eau est à l'état liquide) 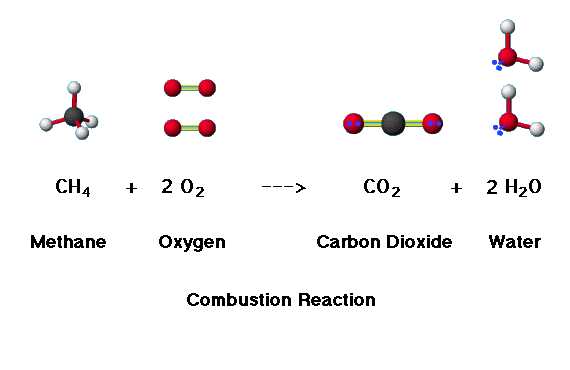 1 mole de méthane (CH4), soit 12x1 + 1x4 = 16g, fournit donc 803 kJ, soit 0,223 kWh. 1 kg de méthane fournit donc 0,223 . 1000/16 = 13.9 kWh La masse volumique du méthane (15 °C,1 bar,gaz) est de 0,6709 kg/m3 1 m3 de méthane fournit donc en brûlant 0,67 kg . 13.9 kWh/kg = 9,3 kWh La combustion d'1 m3 de méthane à 15 °C (gaz naturel) libère une énergie de 9,3 kWh (3.5 MJ). Ce calcul est une bonne approximation pour le gaz de ville, bien qu'il ne soit pas composé à 100% de méthane, et dont la combustion n'est pas intégralement complète. * * * D'autre réaction existent, comme en chimie nucléaire, des réaction de fission ou de fusion. Il y a d'abord la réaction de fission... dans laquelle un atome se brise en 2 parties... ... et libère une énergie énorme de 200 millions d'électron-volt (l'électron-volt c'est une unité d'énergie au niveau atomique qui vaut 1,6 10-19 Joules) Uranium 235 + 1 neutron → Strontium 94 + Xénon 139 + 3 neutrons + énergie c'est à dire : 23592U + 10n → 9438Sr + 13954Xe + 3 10n + 200 Mev ou encore du Krypton et du Baryum 23592U + 10n → 9336Kr + 14056Ba + 2 10n + 200 Mev ou encore 23592U + 10n → 9236Kr + 14156Ba + 3 10n + 200 Mev ou encore du Brome et du Lanthane 23592U + 10n → 8535Br + 14857La + 3 10n + 200 Mev  Sachant que 1 ev = 1électron volt = 1,6 10-19 Joules et que 1 mole d'Uranium 235 = 6,023 10+23 atome d'uranium 235 = 235 g Alors, dans les réactions ci-dessus, 1g d'Uranium consommé entraîne la production de : 200/235 . 10+6 . 1,6 10-19 . 6,023 10+23 = 8,2 10+10 Joules, soit 8,2/3600 10+10 = 23 10+6 Wh = 23000 kWh * * * On peut calculer cette quantité d'énergie produite (ici estimée à 200 MeV) 23592U + 10n → 9438Sr + 13954Xe + 3 10n + quelle quantité d'énergie ? perte de masse = 1 m(23592U) + 1 m(1n) – [1 (m(9438Sr) + 1 (m(13954Xe) + 3 m(1n)] perte de masse = (234,9934 + 1,0087) - (138,8883 + 93,8941 + 3x 1,0087) = 0,1936 u = 0,321376 x 10-27 kg car u est l'unité de masse atomique, et est égal à la masse de 1/12 de la masse d'un atome de carbone 12, et vaut approximativement 1,66 × 10-27 kg Le défaut de masse de 0,1936 u correspond à la fission d'un atome d'Uranium 235. Δm =0,321376 . 10-27 Kg Ceci correspond à une énergie de ΔE = Δm. C2 en calculant : ΔE = (0,321376 x 10-27 kg) x (3,0 . 10+8 m/s)² , soit ΔE =2.892384 · 10-11 J Sachant que 1 ev = 1électron volt = 1,6 10-19 Joules , 1 Mégaélectronvolt (MeV) = 1 MeV = 1,602 18.10–13 Joules ΔE = 289/1.6 MeV, soit : ΔE =181 MeV ~= 200 MeV * * * Ce sont ces réactions qui se sont produites lors de l'explosion atomique de Hiroshima le 6 aout 1945 Ce sont ces réactions qui se produisent de manière contrôlée dans nos centrales nucléaires La combustion de 1 kg de charbon produit 6 kWh environ, à 8 kWh maximum donc 4000 kg de charbon produit donc 22200 kWh environ La fission de 1 gramme d'Uranium produit autant d'énergie que la combustion de ... 3 à 4 tonnes de charbon... ... et sans dégager de CO2 ! Ces réactions de fission, même domestiquées, ne sont pas sans danger. Le danger principal est la fonte du coeur, qui peut se produire dans des conditions extrèmes, comme à Tchernobyl ou Fukushima. Pour copmprendre le déroulement de l'accident de Fukushima, voir la vidéo : "Déroulement de l'Accident de Fukushima Daiichi" La raréfaction des ressources énergétiques fossiles devraient cependant booster le développement du nucléaire, d'abord le nucléaire de 3ème génération (les EPR, ou l'accent est mis sur la sécurité), mais surtout, le nucléaire de 4ème génération, à l'image du projets ASTRID (le successeur des Surgénérateur type Phénix et Superphénix), qui utilisera comme combustible, en lieu et place de l'Uranium 235 : l'Uranium 238, c'est à dire l'Uranium naturel, 100 fois plus abondant que l'Uranium 235. Donc, pendant une durée ... beaucoup plus longue ! RV en 2026 ! Théoriquement, le Nucléaire 4G sera la dernière étape avant la Fusion, qui verra peut être le jour en 2050. A suivre ... * * * Il y a ensuite la réaction de Fusion nucléaire (comme sur le soleil) : Deutérium + Tritium → Hélium + neutron + énergie c'est à dire : 2H + 3H → 4He + 1n + 17.6 Mev  Sachant que 1 ev = 1électron volt = 1,6 10-19 Joules et que 1 mole de deutérium = 6,023 10+23 atome de deutérium = 1g Alors, dans la réaction équilibrée ci-dessus, 1g de deutérium consommé entraîne la production de : 17.6 . 10+6 . 1,6 10-19 . 6,023 10+23 = 170 10+10 Joules, soit 170/3600 10+10 = 444 10+6 Wh = 444 000 kWh La combustion du Charbon donne une quantité d'énergie de 15 à 27 MJ/kg soit pour 1 kg environ 20 10+6 Joules, soit 20/3600 10+6 = 5555 Wh =6 kWh environ, et 8 kWh au maximum donc 78 tonnes de charbon produit donc 444 000 kWh La fusion de 1 gramme de deuterium et d'un gramme de tritium produit autant d'énergie que la combustion de ... 70 à 80 tonnes de charbon ! * * * En fait, la répartition de l'énergie produite est un peu plus subtile 2H + 3H → (4He + énergie cinétique de 3.5 Mev) + (1n + énergie cinétique de 14.1 Mev) On peut calculer cette quantité d'énergie produite. 2H + 3H → 4He + 1n + quelle quantité d'énergie ? perte de masse = 1 m(2H) + 1 m(3H) – [1 (m(4He) + 1 m(1n)] perte de masse = 2,014101777 + 3,016049200 – [4,002602 + 1,0086649] = 0,0188840774 u u est l'unité de masse atomique, et est égal à la masse de 1/12 de la masse d'un atome de carbone 12, et vaut approximativement 1,66 × 10-27 kg Le défaut de masse de 0,01889 u correspond à la fusion d'un atome de deutérium. Δm = 0,01889 . 1,6605 . 10-27 Kg Ceci correspond à une énergie de ΔE = Δm. C2 en calculant : ΔE = (0,01889 . 1,6605.10-27 kg) x (3,0 . 10+8 m/s)² , soit ΔE =2,819 · 10-12 J Sachant que 1 ev = 1électron volt = 1,6 10-19 Joules , 1 Mégaélectronvolt (MeV) = 1 MeV = 1,602 18.10–13 Joules ΔE = 28.19/1.6 Mev, soit : ΔE = 17.6 MeV Dans la pratique, dans la réaction de fusion, on essaie de récupérer l'énergie cinétique du neutron (ici : 14.1 Mev) * * * On comprend que la bombe H (bombe hydrogène, basée sur la fusion), soit terriblement plus puissante que la bombe A (basée sur la fission, comme à Hiroshima - fission de l'Uranium - ou Nagasaki - fission du Plutonium) Tsar Bomba, 57 Mt, fut testée par les russes le 30 octobre 1961 dans un archipel de l'océan arctique. Il s'agit de la plus grande explosion nucléaire de l'histoire. Si une telle bombe H (3000 fois Hiroshima) explosait au dessus de Paris, l'effet serait le suivant...  Les bombes d'aujourd'hui seraient parait-il deux fois moins puissante... Cette réaction de fusion n'est pas à ce jour contrôlée, et ne sera vraisemblablement pas "industrielle" avant 1/2 siècle... dans un petit réacteur expérimental... si nos sociétés vont jusque là... Voir en particulier les projets de fusion : la fusion par confinement imagnétique avec le projet lTER, via le Tokamak en construction à Cadarache ici et là , ou la fusion par confinement inertiel, avec le projet HiPER, via le Laser Mégajoule d'Aquitaine, ici et là) - - - 1 m3 d'océan contient 33g de deutérium, soit, si tout ce deutérium est consommée dans une réaction de fusion, ce m3 d'océan contient l'équivalent en énergie de 33 x 375000 kWh = 12 375 000 kWh 1 tonne équivalent pétrole, c'est 11630 kWh, donc 12 375 000 kWh, c'est 12 375 000 / 11630 = 1064 tep de quoi donner de l'énergie à 600 logements pendant 1 an ! |
| L'énergie de l'homme thermique et mécanique * * * Je rappelle dans ce qui suit les éléments permettant de bien comprendre comment se calcule l'énergie que peut fournir un humain, et combien l'énergie très supérieure fournie par le charbon, le pétrole ou le gaz ont structurés notre monde. Consommation et production thermique d'un homme au repos Un humain consomme environ 2000 Calories alimentaires /jour, sachant qu'une Calorie alimentaire fait 1000 calories. Notre humain consomme donc 2000 Kcal/jour, soit 8360000 Joules/jour (1 calorie = 4.18 joules = 4.18 W.s) En Watt heure, sela nous donne 3600 fois moins, soit 2.32 Kwh/journée de 24 heures. Ainsi un homme au repos consomme en une journée environ 2.5 Kwh, qu'il restitue en grande partie sous forme de chaleur corporelle. Cette énergie est voisine de l'énergie consommée par une ampoule de 100 Watt allumée durant 24 heures. Notre homme d'environ 70kg à donc une puissance thermique de 100 W, soit environ 1,5 Watt par kilogramme. A noter qu'un boeuf de 700 kilogrammes produira une énergie thermique 10 fois supérieure, soit 1000 Watt .... un bon radiateur ! Et les boeuf servait depuis toujours à réchauffer l'étable. Songez à la crèche et au boeuf et à l'âne, produisant leur 2000 W pour réchauffer le petit Jésus !  Un homme au repos, c'est 100 W d'énergie thermique, soit 2.5 kWh par jour. * * * Production d'énergie mécanique avec les jambes Prenons notre homme de 70 kg, demandons lui de gravir 2000 m de dénivelé avec 30 kg sur le dos, afin d'aller reapprovisioner un chalet. L'énergie potentielle de notre homme : Ep=m.g.h variera de ΔEp=m.g.Δh = (70+30) . 9,81 . 2000 = 1962000 Joules, soit 545 Wh. Cette variation d'énergie est intégralement le fruit du travail mécanique de ses jambes.  Ces 545 Wh produit en une bonne journée de labeur représentent une puissance mécanique de 22.7 W, soit environ 25 Watt. Un homme effectuant un travail mécanique avec ses jambes, c'est donc 25 W d'énergie mécanique, et 0.5 kWh par jour.
* * * Production d'énergie mécanique avec les bras Prenons notre homme de 70 kg, demandons lui maintenant de creuser une tranchée de 1 m de profondeur. Il va pour cela remonter de la terre sur une hauteur de 1 m. A une pelleté de 3 kg de terre toute les 5 secondes, et cela pendant 8 heures, cela nous fait 3 / 5 . 3600 . 8 = 17280 kg de terre. L'énergie potentielle de la quantité de terre remontée par notre homme : Ep=m.g.h variera de ΔEp=m.g.Δh = 17280 . 9,81 . 1 = 169517 Joules, soit 47 Wh. Cette variation d'énergie est intégralement le fruit du travail mécanique de ses bras. Ces 50 Wh produit en une bonne journée de labeur représentent une puissance mécanique moyenne sur la journée d'environ 2 Watt. (en fait, sur une journée de travail de 8 h, cela représente 6 Watt durant la phase de travail, sachant qu'il passe le reste de la journée à récupérer) Un homme effectuant un travail mécanique avec ses bras, c'est donc 2 W d'énergie mécanique, et 0.05 kWh par jour.
* * * Et l'énergie du charbon, du gaz, du pétrole ? Comparativement, cela donne quoi ? Ci-dessus, vous avez vu que la combustion d'1 m3 de méthane libèrait une énergie de 10 kWh environ. Il en est de même pour 1 litre d'essence Donc 1 Litre d'essence donne autant d'énergie que ... 10/0.05 = 200 paires de bras !
1 Ch = 736 W Prenons une pelleteuse Caterpillar 365C L, de 72 tonnes, avec un godet de 4,6 m3, Sa puissance disponible P est de 302 kW (kiloWatt), soit 410 ch (chevaux). Elle peut creuser jusqu'à 7 m, et supporter une charge de 5 tonnes de roches (voir ici) Cette pelleteuse de 303 kW tourne 8 heures, et fournit une énergie de 303. 8 = environ 2500 kWh. Elle aura consommé pour cela une centaine de litres de fuel par heure... soit environ 8000 kWh en 8h. Avec un rendement du moteur thermique autour de 30 à 40% (45% pour le moteur seul sans le levage), on retombe aux alentour de nos 2500 kWh, Ces 2500 kWh/jour sont à comparer aux jambes de notre homme (0.5 kWh/jour) ou à ses bras (0.05 kWh/jours), soit 5000 paires de jambes, ou 50 000 paires de bras. C'est élevé. C'est un ordre de grandeur. Une manière de calculer plus en faveur de notre homme, en partant du travail fournit par cette pelleteuse, donc la puissance utilisée pour un travail bien défini : à 4 cycles/minutes (3 à 6) soit 250 cycles à l'heure max, cette pelleteuse, avec son godet de 4,6 m3, aura soulevé 250 . 4,6 = environ 1000 m3 de matériau/heure, soit environ 1500 T/heure (densité 1.5), soit 12 000 T en 8 heures, sur environ 7 mètres de hauteur. A comparer avec nos 17 T soulevées sur 1 m par notre homme, soit 17/7 = 2.5 T sur 7 m, soit 5000 fois plus La pelleteuse en question, comme sur la photo, fournit dans ce cas précis autant d'énergie que ... 5000 paires de bras ! Avec les pelleteuses géantes, on augmente d'un facteur 10 ce ratio. De la même manière, un tracteur agricole de 100 ch (le quart de notre pelleteuse), fournit en traction autant d'énergie qu'un millier de paires de jambes ! * * *
|











